
Image by Author
Deep Learning and Neural Networks consist of interconnected nodes, where data is passed sequentially through each hidden layer. However, the composition of linear functions is inevitably still a linear function. Activation functions become important when we need to learn complex and non-linear patterns within our data.
The two major benefits of using activation functions are:
Introduces Non-Linearity
Linear relationships are rare in real-world scenarios. Most real-world scenarios are complex and follow a variety of different trends. Learning such patterns is impossible with linear algorithms like Linear and Logistic Regression. Activation functions add non-linearity to the model, allowing it to learn complex patterns and variance in the data. This enables deep learning models to perform complicated tasks including the image and language domains.
Allow Deep Neural Layers
As mentioned above, when we sequentially apply multiple linear functions, the output is still a linear combination of the inputs. Introducing non-linear functions between each layer allows them to learn different features of the input data. Without activation functions, having a deeply connected neural network architecture will be the same as using basic Linear or Logistic Regression algorithms.
Activation functions allow deep learning architectures to learn complex patterns, making them more powerful than simple Machine Learning algorithms.
Let’s look at some of the most common activation functions used in deep learning.
Commonly used in binary classification tasks, the Sigmoid function maps real-numbered values between 0 and 1.
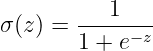
The above equation looks as below:
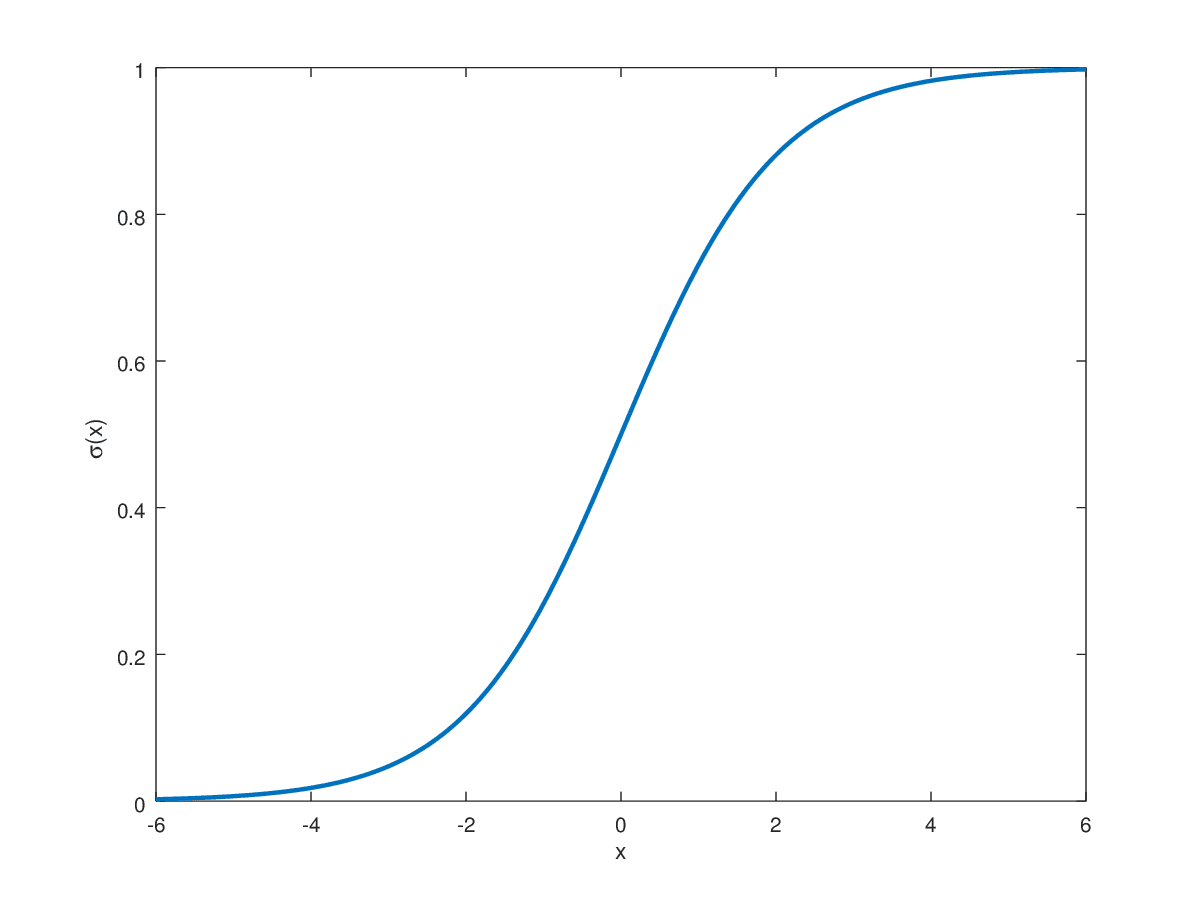
Image by Hvidberrrg
The Sigmoid function is primarily used in the output layer for binary classification tasks where the target label is either 0 or 1. This naturally makes Sigmoid preferable for such tasks, as the output is restricted between this range. For highly positive values that approach infinity, the sigmoid function maps them close to 1. On the opposite end, it maps values approaching negative infinity to 0. All real-valued numbers between these are mapped in the range 0 to 1 in an S-shaped trend.
Shortcomings
Saturation Points
The sigmoid function poses problems for the gradient descent algorithm during backpropagation. Except for values close to the center of the S-shaped curve, the gradient is extremely close to zero causing problems for training. Close to the asymptotes, it can lead to vanishing gradient problems as small gradients can significantly slow down convergence.
Not Zero-Centered
It is empirically proven that having a zero-centered non-linear function ensures that the mean activation value is close to 0. Having such normalized values ensures faster convergence of gradient descent towards the minima. Although not necessary, having zero-centered activation allows faster training. The Sigmoid function is centered at 0.5 when the input is 0. This is one of the drawbacks of using Sigmoid in hidden layers.
The hyperbolic tangent function is an improvement over the Sigmoid function. Instead of the [0,1] range, the TanH function maps real-valued numbers between -1 and 1.
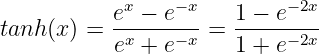
The Tanh function looks as below:
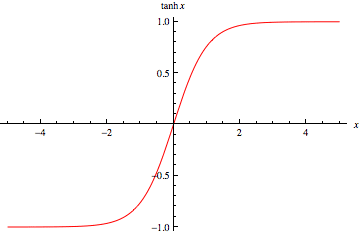
Image by Wolfram
The TanH function follows the same S-shaped curve as the Sigmoid, but it is now zero-centered. This allows faster convergence during training as it improves on one of the shortcomings of the Sigmoid function. This makes it more suitable for use in hidden layers in a neural network architecture.
Shortcomings
Saturation Points
The TanH function follows the same S-shaped curve as the Sigmoid, but it is now zero-centered. This allows faster convergence during training improving upon the Sigmoid function. This makes it more suitable for use in hidden layers in a neural network architecture.
Computational Expense
Although not a major concern in the modern day, the exponential calculation is more expensive than other common alternatives available.
The most commonly used activation function in practice, Rectified Linear Unit Activation (ReLU) is the most simple yet most effective possible non-linear function.
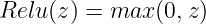
It conserves all non-negative values and clamps all negative values to 0. Visualized, the ReLU functions look as follows:
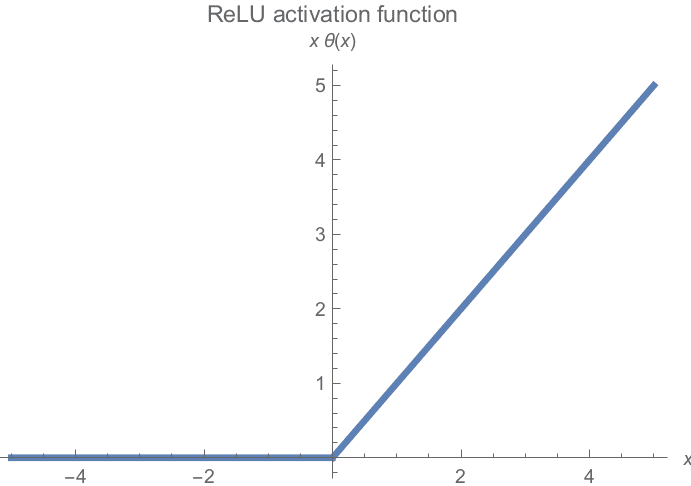
Image by Michiel Straat
Shortcomings
Dying ReLU
The gradient flattens at one end of the graph. All negative values have zero gradients, so half of the neurons may have minimal contribution to training.
Unbounded Activation
On the right-hand side of the graph, there is no limit on the possible gradient. This can lead to an exploding gradient problem if the gradient values are too high. This issue is normally corrected by Gradient Clipping and Weight Initialization techniques.
Not Zero-Centered
Similar to Sigmoid, the ReLU activation function is also not zero-centered. Likewise, this causes problems with convergence and can slow down training.
Despite all shortcomings, it is the default choice for all hidden layers in neural network architectures and is empirically proven to be highly efficient in practice.
Now that we know about the three most common activation functions, how do we know what is the best possible choice for our scenario?
Although it highly depends on the data distribution and specific problem statement, there are still some basic starting points that are widely used in practice.
- Sigmoid is only suitable for output activations of binary problems when target labels are either 0 or 1.
- Tanh is now majorly replaced by the ReLU and similar functions. However, it is still used in hidden layers for RNNs.
- In all other scenarios, ReLU is the default choice for hidden layers in deep learning architectures.
Muhammad Arham is a Deep Learning Engineer working in Computer Vision and Natural Language Processing. He has worked on the deployment and optimizations of several generative AI applications that reached the global top charts at Vyro.AI. He is interested in building and optimizing machine learning models for intelligent systems and believes in continual improvement.

