This blog post is available as a jupyter notebook on GitHub.
Augmentations have become an indispensable component in the realm of computer vision pipelines. However, their popularity hasn’t reached the same heights in other domains, such as time series. In this tutorial, I will delve into the world of time series augmentations, shedding light on their significance and providing concrete examples of their application using the powerful generative time series modeling library, TSGM [5].
Our starting point is a dataset denoted (????, ????). Here, ????ᵢ ∈ ???? are multivariate (meaning, each time point is a multiple dimensional feature vector) time series, and y are labels. Predicting labels y is called a downstream task. Our goal is to use (????, ????) to produce additional samples (????*, ????*), which could help us solve the downstream task more effectively (in terms of predictive performance or robustness). For simplicity, we won’t work with labels in this tutorial, but the methods we describe here are straightforward to generalize to the case with labels, and the software implementations we use are easily extended to the supervised case by adding additional parameters to the .generate method (see examples below).
Without further ado, let’s consider time series augmentations one by one.
In TSGM, all augmentations are neatly organized in tsgm.models.augmentations, and you can check out the comprehensive documentation available at TSGM documentation.
Now, let’s kickstart coding examples by installing tsgm:
pip install tsgm
Moving forward, we import tsgm, and load an exemplary dataset. A tensor X now contains 100 sine time series of length 64, with 2 features each. With random shift, frequencies, and amplitudes (maximum amplitude is 20).
# import the libraries
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import random
from tensorflow import keras
import tsgm
# and now generate the dataset
X = tsgm.utils.gen_sine_dataset(100, 64, 2, max_value=20)
First, as the first augmentation we consider jittering.
Time series data are augmented with random Gaussian noise (Wikipedia)
In tsgm, Gaussian noise augmentation can be applied as follows:
aug_model = tsgm.models.augmentations.GaussianNoise()
samples = aug_model.generate(X=X, n_samples=10, variance=0.2)
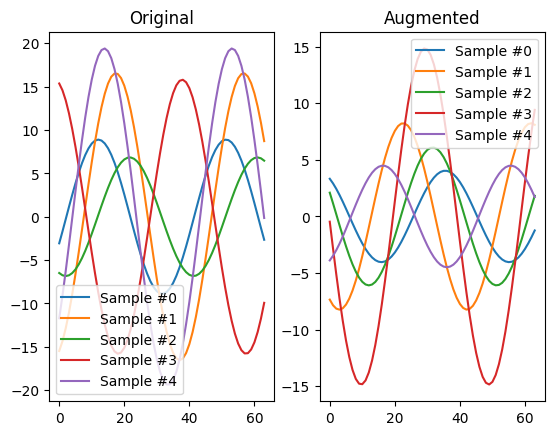
The idea behind Gaussian noise augmentation is that adding a small amount of jittering to time series probably will not change it significantly but will increase the amount of such noisy samples in our dataset. It often makes the downstream models more robust to noisy samples or improves predictive performance.
The hyperparameters of Gaussian noise and the way of adding the noise (e.g., Gaussian noise can increase towards the end of a time series) is a difficult question and depends on a particular dataset and downstream problem. It is often worth experimenting and seeing how those parameters affect the performance of the target model.
Here, we provide a visualization of samples from the original sine dataset and augmented samples.
Another approach to time series augmentation is simply shuffle the features. This approach is suitable only for particular multivariate time series, where they are invariant to all or particular permutations of features. For instance, it can be applied to time series where each feature represents same independent measurements from various sensors.
To explain this approach, let’s take the example of five identical sensors, labeled as S_1, S_2, S_3, S_4, and S_5. For the sake of illustration, let’s assume that sensors 1–4 are probably exchangeable with respect to rotations. Then it makes sense to try augmenting data with feature rotations with respect to rotations of S_1, …, S_5 sensors.
Similarly to the previous example, the augmentation can work as follows:
aug_model = tsgm.models.augmentations.Shuffle()
samples = aug_model.generate(X=X, n_samples=3)
Here, we show one sample from a timeseries with 5 features, and an augmented sample, analogously to the image above.
Slice and shuffle augmentation [3] cuts a time series into slices and shuffles those pieces. This augmentation can be performed for time series that exhibit some form of invariance over time. For instance, imagine a time series measured from wearable devices for several days. The good strategy for this case is to slice time series by days and, by shuffling those days, get additional samples. Slice and shuffle augmentation is visualized in the following image:
aug_model = tsgm.models.augmentations.SliceAndShuffle()
samples = aug_model.generate(X=X, n_samples=10, n_segments=3)
Let’s view augmented and original samples:
Magnitude warping [3] changes the magnitude of each sample in a time series dataset by multiplication of the original time series with a cubic spline curve. This process scales the magnitude of time series, which can be beneficial in many cases, such as our synthetic example with sines n_knots number of knots at random magnitudes distributed as N(1, σ^2) where σ is set by a parameter sigma in function .generate.
aug_model = tsgm.models.augmentations.MagnitudeWarping()
samples = aug_model.generate(X=X, n_samples=10, sigma=1)
Here is an example of original data and augmented samples generated with MagnitudeWarping.
In this technique [4], the selected windows in time series data are either speeding up or down. Then, the whole resulting time series is scaled back to the original size in order to keep the timesteps at the original length. See an example of such augmentation below:
Such augmentation can be beneficial, e.g., in modeling equipment. In such applications, sensor measurements can change the speed of change depending on how those pieces of equipment are used.
In tsgm, as always, the generation can be done via
aug_model = tsgm.models.augmentations.WindowWarping()
samples = aug_model.generate(X=X, n_samples=10, scales=(0.5,), window_ratio=0.5)
An example of a generated time series can be found below.
Dynamic Time Warping Barycentric Average (DTWBA)[2] is an augmentation method that is based on Dynamic Time Warping (DTW). DTW is a method of measuring similarity between time series. The idea is to “sync” those time series, as it is demonstrated in the following picture.
More details on DTW computation are available at https://rtavenar.github.io/blog/dtw.html.
DTWBA goes like this:
1. The algorithm picks one time series to initialize the DTWBA result. This time series can either be given explicitly or can be chosen randomly from the dataset
2. For each of the N time series, the algorithm computes DTW distance and the path (the path is the mapping that minimizes the distance)
3. After computing all N DTW distances, the algorithm updates the DTWBA result by doing the average with respect to all the paths found above
4. The algorithm repeats steps (2) and (3) until the DTWBA result converges
A reference implementation can be found in tslearn, and a description can be found in [2].
In tsgm, the samples can be generated as follows
aug_model = tsgm.models.augmentations.DTWBarycentricAveraging()
initial_timeseries = random.sample(range(X.shape[0]), 10)
initial_timeseries = X[initial_timeseries]
samples = aug_model.generate(X=X, n_samples=10, initial_timeseries=initial_timeseries )
Another approach to augmentation is to train a machine learning model on historical data and train it to generate novel synthetic samples. It is a blackbox method because it is hard to interpret how new samples were generated. Several methods can be applied in the case of time series; in particular, tsgm has VAE, GANs, and Gaussian processes. An example of the generation of synthetic time series with VAEs is
n, n_ts, n_features = 1000, 24, 5
data = tsgm.utils.gen_sine_dataset(n, n_ts, n_features)
scaler = tsgm.utils.TSFeatureWiseScaler()
scaled_data = scaler.fit_transform(data)
architecture = tsgm.models.zoo[“vae_conv5”](n_ts, n_features, 10)
encoder, decoder = architecture.encoder, architecture.decodervae = tsgm.models.cvae.BetaVAE(encoder, decoder)
vae.compile(optimizer=keras.optimizers.Adam())
vae.fit(scaled_data, epochs=1, batch_size=64)
samples = vae.generate(10)
We explored several methods for synthetic time series generation. Many of them introduce inductive biases into the model and are useful in practical settings.
How to choose? First, analyze whether your problem contains invariances. Is it invariant to random noise? Is it invariant to feature shuffling?
Next, choose a broad set of methods and verify whether any of the selected methods improve the performance of your downstream problem (tsgm has downstream performance metric). Then, select the set of augmentation methods that gives the largest performance boost.
Last, but not least, I thank Letizia Iannucci and Georgy Gritsenko for help and useful discussions about writing of this post. Unless otherwise noted, all images are by the author.
This blog post is a part of the project TSGM, in which we are creating a tool for enhancing time series pipelines via augmentation and synthetic data generation. If you found it helpful, take a look at our repo and consider citing the paper about TSGM:
@article{
nikitin2023tsgm,
title={TSGM: A Flexible Framework for Generative Modeling of Synthetic Time Series},
author={Nikitin, Alexander and Iannucci, Letizia and Kaski, Samuel},
journal={arXiv preprint arXiv:2305.11567},
year={2023}
}
[1] H. Sakoe and S. Chiba, “Dynamic programming algorithm optimization for spoken word recognition”. IEEE Transactions on Acoustics, Speech, and Signal Processing, 26(1), 43–49 (1978).
[2] F. Petitjean, A. Ketterlin & P. Gancarski. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognition, Elsevier, 2011, Vol. 44, Num. 3, pp. 678–693
[3] Um TT, Pfister FM, Pichler D, Endo S, Lang M, Hirche S,
Fietzek U, Kulic´ D (2017) Data augmentation of wearable sensor data for parkinson’s disease monitoring using convolutional neural networks. In: Proceedings of the 19th ACM international conference on multimodal interaction, pp. 216–220
[4] Rashid, K.M. and Louis, J., 2019. Window-warping: a time series data augmentation of IMU data for construction equipment activity identification. In ISARC. Proceedings of the international symposium on automation and robotics in construction (Vol. 36, pp. 651–657). IAARC Publications.
[5] Nikitin, A., Iannucci, L. and Kaski, S., 2023. TSGM: A Flexible Framework for Generative Modeling of Synthetic Time Series. arXiv preprint arXiv:2305.11567. Arxiv link.