GNNs Explained Series
Connecting the dots for a theoretical analysis of Graph Neural Network models
This series aims to provide a comprehensive understanding of how GNNs capture the relational information of network structures.
Graphs represent universal models to describe interacting elements, and Graph Neural Networks (GNNs) have become an essential toolkit for applying learning algorithms to graph-structured data.
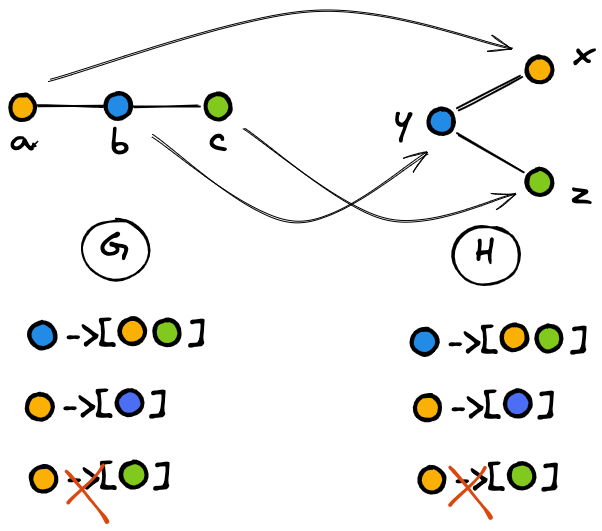
The most common framework of GNNs is based on the Message Passing Neural Network (MPNN). In this framework, the neighbor features are passed to the target node as messages through the edges. Then, the target node representation is updated with the aggregated representation of its neighbors.
Based on this principle, the new representation of the node encodes information related to the local structure. This message-passing procedure is illustrated in Figure 1.
This Figure shows how the representation of the orange node is updated, aggregating its neighbors’ features. More specifically, by stacking a single MPNN layer, the orange node is updated with the representation of the blue nodes. Adding one more layer, the resulting representation of the orange node incorporates the features of blue and green nodes.
For the sake of simplicity, we are considering only the aggregation performed on the orange node. However, this computation is executed in parallel for all the nodes in the graph, including the blue and the green nodes, whose representation is updated with their neighbor (including the orange one!) features.
The main difference between diverse GNN models lies in the type of feature aggregation executed to update the node representation. The neighbor features can be aggregated using a sum or an average operation, as in the case of Graph Convolutional Networks (GCNs) and GraphSage. In other cases, such as Graph Attention Networks (GATs), we can add a further step in which the contribution of each neighbor node is weighted according to its importance.
